Tworzenie szaty graficznej.

Jeśli znasz choć trochę aplikację Excel, arkusze GOOGLE lub inny arkusz kalkulacyjny wiesz, że nie wygląda on zbyt zachęcająco na pierwszy rzut oka. Całe obszar roboczy zajmuje jedna wielka tabela. Aby wprowadzić więcej życia w ten program, zachęcam Cię do zabawy grafiką.
Wystarczy skorzystać z dowolnej aplikacji desktopowej lub webowej, którą lubisz i znasz do narysowania elementów jak przyciski, ramki i różne dekoracje, które sprawią, że praca, którą wykonasz nie będzie bezduszną tabelą. Będzie wyglądała jak profesjonalna aplikacja, magnetyzująca graficznie i zachęcająca do pracy, nauki lub zabawy. Pod warunkiem oczywiście, że narysujesz to starannie i estetycznie...

Skąd mam znać wymiary rysunków?

To bardzo ważne pytanie, które powinno zrodzić się w Twojej głowie zanim zaczniesz rysować cokolwiek. To bardzo ważny etap, najpierw musisz wyobrazić sobie co chcesz stworzyć, najlepiej narysować sobie to fizycznie, zwymiarować, a dopiero później tworzyć cokolwiek w komputerze.

Na szczęście w Excelu łatwo sprawdzić jak dużo zajmuje jedna komórka (z dokładnością do jednego pixela). Spójrz na rysunek poniżej:

Powyższy obrazek pokazuje czym jest skala. Niezależnie od tego czy tworzysz coś w skali w rzeczywistości czy w programie komputerowym, musisz pamiętać o skali i wszystko wcześniej przygotować. Analizując powyższy obrazek łatwo dostrzec, że każdy z elementów jest względem pozostałych podobny w skali. Dla przykładu szerokość i wysokość domu względem szerokości i wysokości pojedynczego okna są obliczone na podstawie tego samego współczynnika - skali. Dzięki temu całość wygląda realistycznie.

Proporcja

Zanim stworzysz jakikolwiek obiekt, musisz wcześniej obliczyć jego wymiary. Dzięki proporcji, można z góry zaplanować jakie wymiary musi mieć po zmniejszeniu dany obiekt. To najłatwiejsza metoda, którą znasz z matematyki. Załóżmy, że mamy do narysowania biurko o wymiarach:

szerokość: 60cm 
 głębokość: 50cm 
 wysokość: 80cm 

Gdyby narysować w magicavoxel blat tego biurka przy pomocy VOXELI 5x6, a jego nogę na 8 VOXELI, oznaczałoby to że w rzeczywistości 1 VOXEL = 10cm.
Skala się zgadza, tylko należy zadać sobie pytanie, czy to wystarczająca skala?

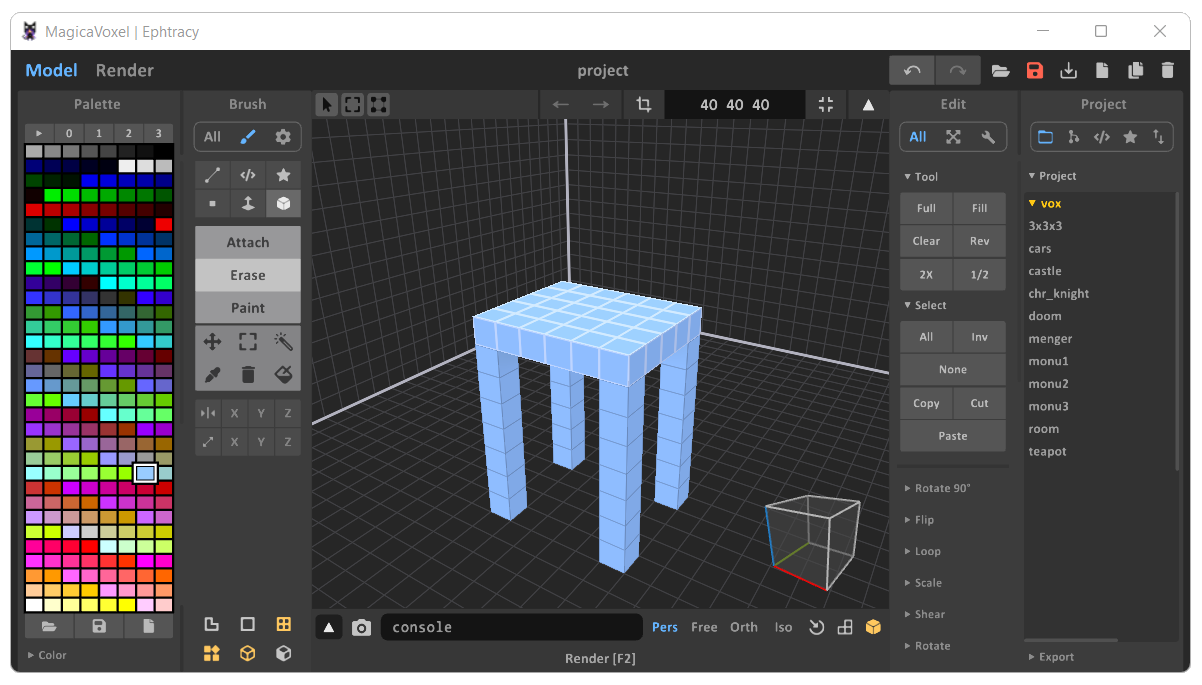
Obrazek własny

Odpowiedź jak zwykle nie jest jednoznaczna - kolejne pytanie: co jeszcze chcemy narysować? Wszystko zależy od tego jak drobne szczegóły chcemy pokazać. Analizując przykład biurka powyżej, zadaj sobie pytanie, czy jesteś w stanie narysować leżącą na blacie gumkę do mazania? Jeśli twierdzisz, że tak to spróbuj znaleźć w sieci gumkę do mazania o wymiarach 10cm x 10cm :) Następnie wyobraź sobie w jaki sposób narysować na tym biurku laptopa i lampkę...

W rzeczywistości wszystko to byłoby możliwe do narysowania na takiej powierzchni. Weź miarę i sprawdź czy Twój laptop zmieściłby się na blacie biurka o takich wymiarach.

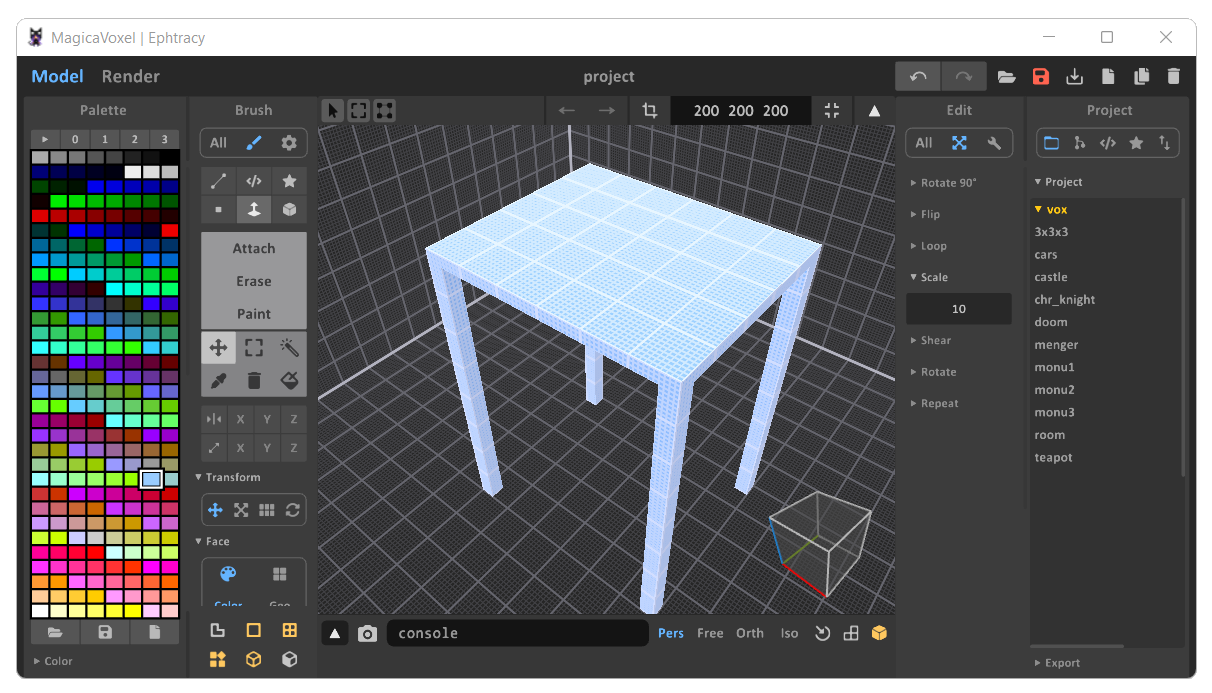
Obrazek własny

To jest dokłanie takie samo biurko z punktu widzenia skali podobieństwa. Jedyną różnicą jest wielkość pojedynczego VOXELA. Zauważ, że dzięki tej operacji zyskaliśmy możliwość zmiany grubości nogi tego biurka. Wcześniej zgodnie z obliczeniami, mogła mieć 10cm, ponieważ taki rozmiar miał 1 VOXEL. Jeśli noga miałaby być większa, mogła by mieć wyłącznie wielokrotność 10, czyli 20cm, 30cm itd.
Teraz, gdy założyliśmy że 1 VOXEL odpowiada 1cm, można pozwolić sobie na znacznie więcej. W przeciwieństwie do pierwszego przykładu, na drugim biurku bez problemu mozna narysować gumkę do mazania, opakowanie z pisakami, a nawet pojedynczy ołówek.
Oczywiście narysowanie czegoś mniejszego niż centymetr nie będzie możliwe. Wtedy trzeba się zastanwić w jaki sposób zmienić bazowy wymiar, by narysowanie obiektu, na którym nam zalezy było możliwe.

UWAGA!